
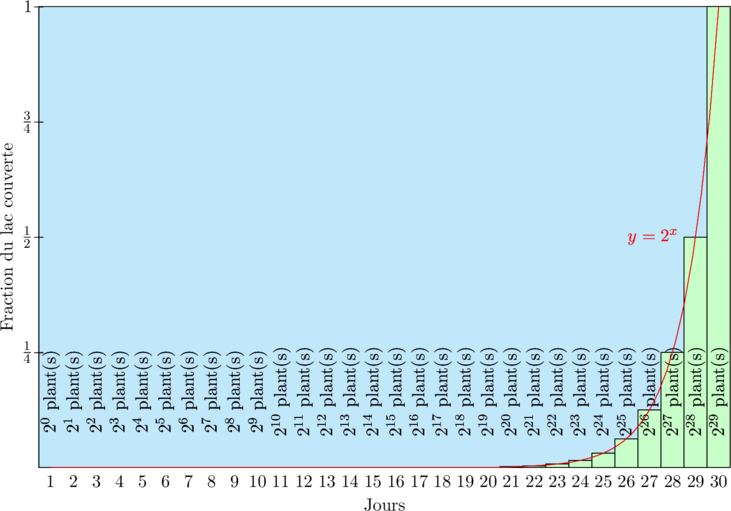
Imaginons un nénuphar planté dans un grand lac qui aurait la propriété héréditaire de produire, chaque jour, un autre nénuphar.
Au bout de trente jours, la totalité du lac est couverte et l’espèce meurt étouffée, privée d’espace et de nourriture.
Au bout de combien de jours les nénuphars ont-ils couvert la moitié du lac ? [1]Albert Jacquard, L’équation du nénuphar, les plaisirs de la science, Calmann-Lévy, 1998
Vous avez compris : le lac était à moitié couvert au bout de 29 jours.
C’est une surprise … ? Réfléchissons en mettant la marche arrière.
Si nous sommes le 29ème jour, le lac est à moitié couvert, donc, demain, le 30ème jour, la surface aura doublé et les nénuphars couvriront l’entièreté du lac.
De même, si nous sommes le 28ème jour, un quart du lac est recouvert, et le lendemain, la moitié le sera … etc.
Donc, lorsqu’un huitième de la surface est couverte, cela paraît rassurant, mais en fait nous sommes à trois jours de la couverture complète …
C’est un exemple d’exponentielle de base 2 : la quantité double chaque jour.
Les mathématiciens aiment mettre cela en formule :
![]()
où
C’est joli, des nénuphars, mais quel rapport avec la Covid 19 ?
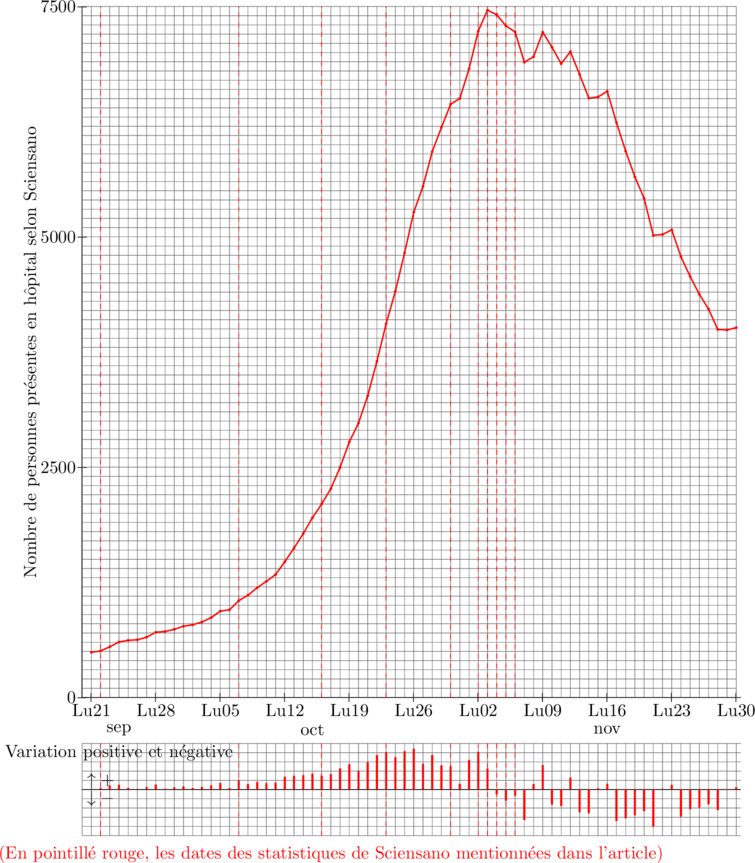
Imaginons une situation : septembre 2020, un hôpital imaginaire, si standard qu’il correspond exactement aux statistiques de Sciensano, un service Covid, 46 places, une partie en soins intensifs. La cheffe du service consulte quotidiennement les statistiques de Sciensano [2]Site des statistiques de Sciensano : https://epistat.wiv-isp.be/covid/covid-19.html, attentive au doublement du nombre de personnes hospitalisées.
Elle écrit sur le tableau du service :
«Nombre de personnes hospitalisées :»
«mardi 22 septembre 2020 – Sciensano : 505 – nous : 3 ![]() (en hausse).»
(en hausse).»
15 jours après, elle écrit :
«mercredi 7 octobre 2020 – Sciensano : 1050 – nous : 6 ![]() .»
.»
La veille, le communiqué officiel du 6 octobre titrait : «Le Comité de concertation décide de mesures plus strictes et désigne un commissaire COVID-19».
9 jours plus tard :
«vendredi 16 octobre 2020 – Sciensano : 2099 – nous : 12 ![]() .»
.»
7 jours après :
«vendredi 23 octobre 2020 – Sciensano : 4056 – nous : 24 ![]()
On suit le mouvement, mais ça double de plus en plus vite.»
Se souvenant de ses cours de mathématiques, elle pense : «c’est pire qu’une exponentielle de base 2, où les intervalles de temps seraient égaux. Notre professeur nous avait parlé de nénuphars …»
Arrive le directeur financier de l’hôpital : «Tout va bien, le service est occupé à … (il calcule vite sur son smartphone) 24 : 46 x 100 =… 52,2 %, il reste presque la moitié de lits disponibles !»
Mais la répartie est immédiate : «Pas du tout, vous n’y êtes pas! Si ça continue ainsi, vendredi prochain, nous serons complets et nous aurons dû trouver un autre hôpital pour deux malades !»
Mais, heureusement, elle peut écrire le vendredi suivant :
«vendredi 30 octobre 2020 – Sciensano : 6439 – nous : 38 ![]()
LE POINT D’INFLEXION EST DÉPASSÉ, ÇA MONTE TOUJOURS
MAIS ÇA RALENTI, L’EFFET DES MESURES SE FAIT SENTIR,
ON VA Y ARRIVER !»
Et elle le répète à tout le monde !!!
Et le vendredi suivant, on peut lire au tableau :
«lundi 2 novembre – Sciensano : 7233 – nous : 43 ![]() »
»
«mardi 3 novembre – Sciensano : 7461 – nous : 44 ![]() »
»
«mercredi 4 novembre – Sciensano : 7411 – nous : 44 ![]() »
»
«jeudi 5 novembre – Sciensano : 7290 – nous : 43 ![]() »
»
«vendredi 6 novembre – Sciensano : 7224 – nous : 43 ![]() »
»
«On a été presque complet, mais maintenant, après un mois d’efforts,
ON A GAGNÉ, ÇA DESCEND !»
Notes
| ↑1 | Albert Jacquard, L’équation du nénuphar, les plaisirs de la science, Calmann-Lévy, 1998 |
|---|---|
| ↑2 | Site des statistiques de Sciensano : https://epistat.wiv-isp.be/covid/covid-19.html |
